Force Coefficient#

The Force Coefficient, $C_f$, is a dimensionless parameter that provides a generalized representation of the resultant forces experienced by an object within a fluid flow. It offers a means to evaluate the cumulative effect of pressure coefficients, $c_p$ across different regions of an object’s surface and how these pressures translate into aerodynamic forces.

$C_f$ is a fundamental tool for assessing lift, drag, and other forces crucial for the design and analysis of aerodynamic components.

Definition#

This coefficient is defined as a net resulting force coefficient of a body. A body is composed by a set of surfaces. For example, consider a building’s canopy, where the lower surface is marked on red, and the upper surface is marked on green:

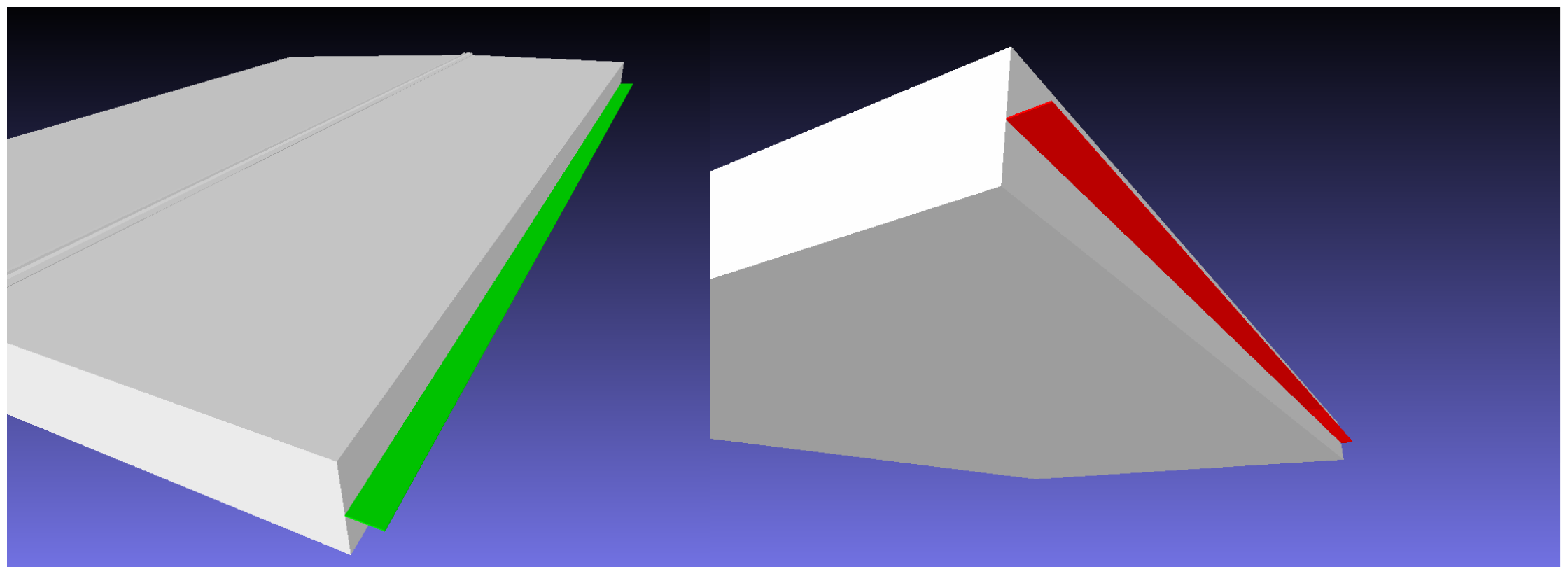
The net resulting force coefficient is defined as:

\[C_{f} = \frac{\sum F_{res}}{q A_{rep}} = \frac{F_{green} + F_{red}}{q A_{rep}} = \frac{\sum{c_{pi} A_{i}} + \sum{c_{pj} A_{j}}}{A_{rep}}\]

Important

Note that the net force coefficient has a direction attached to its definition. Its direction is the same as the resulting force direction.

It can also be defined for each axis direction:

\[C_{fx} = \frac{\sum Fx_{res}}{q A_{x}} = \frac{Fx_{green} + Fx_{red}}{q A_{x}} = \frac{\sum{c_{pi} A_{ix}} + \sum{c_{pj} A_{jx}}}{A_{x}}\]

\[C_{fy} = \frac{\sum Fy_{res}}{q A_{y}} = \frac{Fy_{green} + Fy_{red}}{q A_{y}} = \frac{\sum{c_{pi} A_{iy}} + \sum{c_{pj} A_{jy}}}{A_{y}}\]

\[C_{fz} = \frac{\sum Fz_{res}}{q A_{z}} = \frac{Fz_{green} + Fz_{red}}{q A_{z}} = \frac{\sum{c_{pi} A_{iz}} + \sum{c_{pj} A_{jz}}}{A_{z}}\]

We define the nominal area ($A_x$, $A_y$, $A_z$) as a user input, constant for all axis ($A_x$=$A_y$=$A_z$). This is done to let the user define how they want to calculate its value. The mathematical definition is to use the projection of the surface area for the body composed in the given axis.

Note

For a non constant nominal area, the values of moment coefficient can be generated and later renormalized based on geometry informations.

Use Case#

A common application of the net force coefficient requires sectioning the body in different sub-bodies. To do so, a similar logic applied to the shape coefficient is used to determine the respective sub-body of each of the body’s triangles. If its center lies inside the sub-body volume, then it belongs to it.

The result is a sectionated body in different sub-bodies for each interval. When sectioning the body, the respective nominal area should be the same as the sub-body nominal area.

Note

Check out the definitions section for more information about surface, body and sub-body definitions.

Like the other coefficients, we can apply statistical analysis to the net force coefficient.

By definition, the net force coefficient is a property of a body.

It is used for primary and secondary structures design, such as canopies and roof vents. It can also be used for evaluating the resultant wind action over a building or the building paviments. It can be seen as the resulting effect of the wind induced force over a body.

Artifacts#

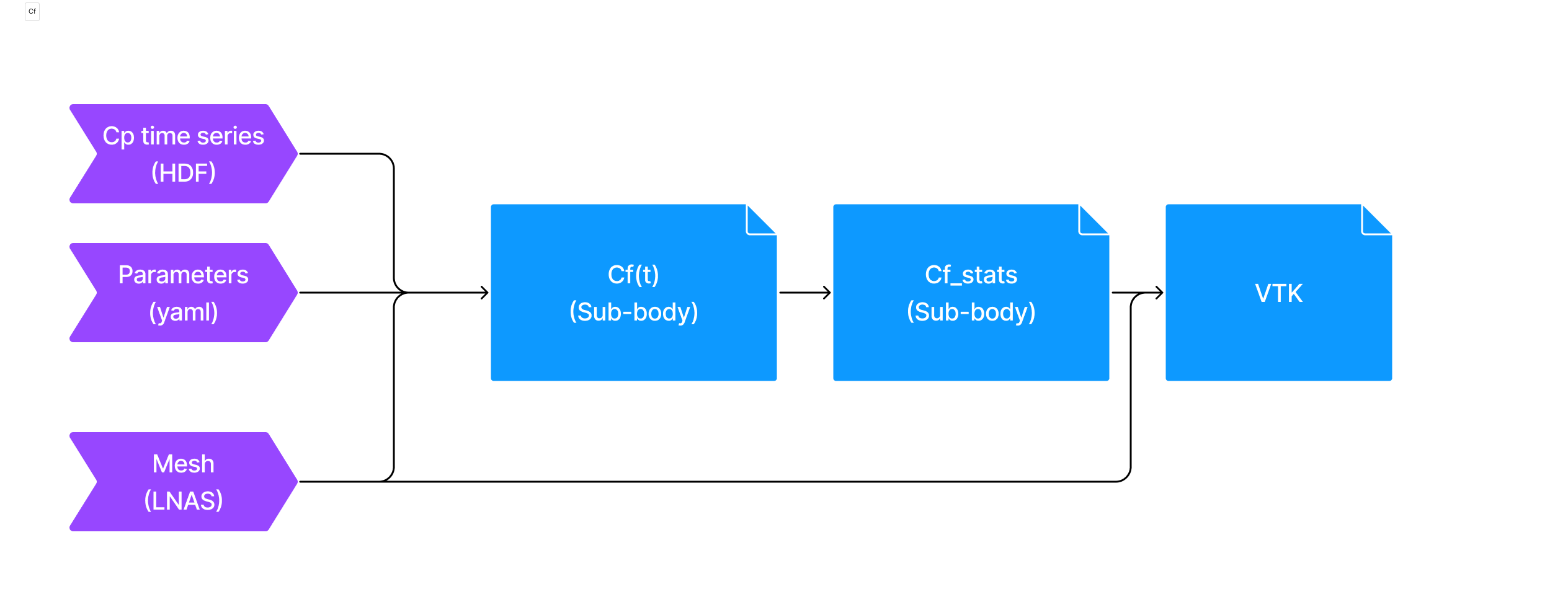
In order to use the force coefficient module, the user has to provide a set of artifacts:

A lnas file: It contains the information about the mesh.
Parameters file: It contains which surface inside the mesh is going to be used for evaluating net force coefficient as well as other configs parameters.
HDF time series: It contains the pressure coefficient signals indexed by each of the mesh triangles.

Which outputs the following data:

Dimensionless time series: force coefficient time series for each body.
Statistical results: maximum, minimum, RMS and average values for the force coefficient time series, for each body.
VTK File: contains the statistical values inside the original mesh (VTK).

An illustration of the force coefficient module pipeline can be seen below:

Usage#

An example of the parameters file required for calculating the net force coefficient can be seen below:

bodies:
  marquise:
    surfaces: [list_of_surfaces_of_marquise]
  lanternim:
    surfaces: [list_of_surfaces_of_lanternim]
  building:
    surfaces: [building]
force_coefficient:
  measurement_1:
    bodies:
      - name: building
        sub_bodies: # Optional, default is the whole body
          z_intervals: [0, 10, 20]
    directions: ["x", "y", "z"]
    statistics:
      - stats: "mean"
      - stats: "rms"
      - stats: "skewness"
      - stats: "kurtosis"
      - stats: "min"
        params:
          method_type: "Absolute"
      - stats: "max"
        params:
          method_type: "Absolute"
    # Apply transformations before indexing the regions
    transformation:
      translation: [0, 0, 0]
      rotation: [0, 0, 0]
      fixed_point: [0, 0, 0]
  measurement_2:
    bodies:
      - name: marquise
    directions: ["x", "y", "z"]
    statistics:
      - stats: "mean"
      - stats: "rms"
      - stats: "skewness"
      - stats: "kurtosis"
      - stats: "min"
        params:
          method_type: "Absolute"
      - stats: "max"
        params:
          method_type: "Absolute"
    # Apply transformations before indexing the regions
    transformation:
      translation: [0, 0, 0]
      rotation: [0, 0, 0]
      fixed_point: [0, 0, 0]

To invoke and run the calculation, the following command can be used:

uv run python -m cfdmod.use_cases.pressure.Cf \
   --output {OUTPUT_PATH} \
   --cp     {CP_SERIES_PATH} \
   --mesh   {LNAS_PATH} \
   --config {CONFIG_PATH}

Or it can be generated together with the pressure data conversion:

uv run python -m cfdmod.use_cases.pressure \
   --output {OUTPUT_PATH} \
   --cp     {CP_SERIES_PATH} \
   --mesh   {LNAS_PATH} \
   --config {CONFIG_PATH} \
   --Cf

Another way to run the force coefficient calculation, is through the notebook

Data format#

Note

The rule for determining the region_idx is based on the region index and the body name. Input mesh can have multiple bodies, and each of them can be applied a specific zoning/region rule. Because of that, region_idx has to be composed by the zoning region index joined by “-” and the body name. This also guarantee that even if different bodies lie on the same region, the interpreted region for each of them will be different

Note

For more information about the normalized time scale ($t^*$), check the Normalization section

$C_{fx}(t)$#
time_idx/region_idx	Normalized time ($t^*$)	0-Body1	1-Body1	0-Body2
0	10000	1.25	1.15	-1.1
1	11000	1.5	0.9	-1.15

$C_{fy}(t)$#
time_idx/region_idx	Normalized time ($t^*$)	0-Body1	1-Body1	0-Body2
0	10000	1.25	1.15	-1.1
1	11000	1.5	0.9	-1.15

$C_{fz}(t)$#
time_idx/region_idx	Normalized time ($t^*$)	0-Body1	1-Body1	0-Body2
0	10000	1.25	1.15	-1.1
1	11000	1.5	0.9	-1.15

$C_{fx} (stats)$#
region_idx	max	min	mean	std	skewness	kurtosis
0-Body1	1.25	0.9	1.1	0.2	0.1	0.15
1-Body1	1.15	0.95	1.13	0.19	0.11	0.13

$C_{fy} (stats)$#
region_idx	max	min	mean	std	skewness	kurtosis
0-Body1	1.25	0.9	1.1	0.2	0.1	0.15
1-Body1	1.15	0.95	1.13	0.19	0.11	0.13

$C_{fz} (stats)$#
region_idx	max	min	mean	std	skewness	kurtosis
0-Body1	1.25	0.9	1.1	0.2	0.1	0.15
1-Body1	1.15	0.95	1.13	0.19	0.11	0.13

$Regions(indexing)$#
region_idx	point_idx
0-Body1	0
1-Body1	1

$Regions(definition)$#
region_idx	x_min	x_max	y_min	y_max	z_min	z_max	Lx	Ly	Lz
0-Body1	0	100	0	50	0	20	0.5	0.8	0.1
1-Body1	100	200	0	50	0	20	0.8	0.5	0.2

Force Coefficient

Contents

Force Coefficient#

Definition#

Use Case#

Artifacts#

Usage#

Data format#