Meshing

The meshing process for Nassu receives a .lnas file and returns a series of points with normal and area. To do that, the triangles are refined up to certain area and then the points are generated. Here it’s described how this process is done.

Refinement

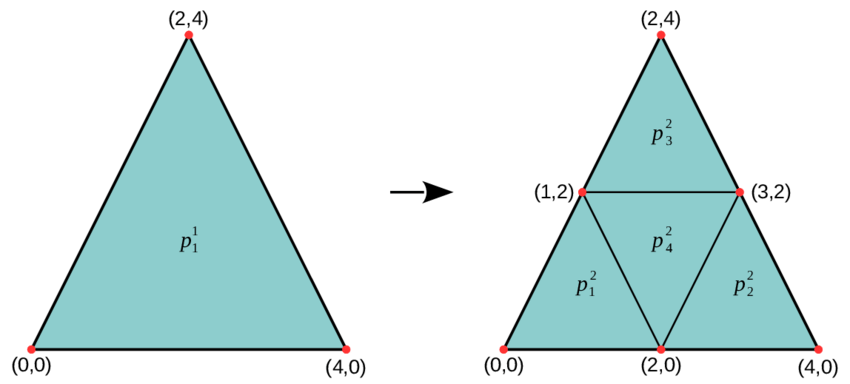
Triangle refinement

The refinement turns a single triangle into 4 similar triangles (with same angles). This preserves the triangle normal and angles and divides the area in 4.

The triangles are refined recursively, up to when it reaches an interval of area provided in the simulation configuration file.

This refinement also considers the block’s level of where the triangle is. So the area of the final triangle in a block of level 2 is 16 times smaller (\(4^2\)) than if it was in a block of level 0.

Vertices generation

After this refinement, the series of points is generated. We call these points vertices. Each vertice has a position, a normal and an area. There are two main ways to generate each vertice for the triangles: central based and vertice based.

Central based uses the triangle center as position and its normal and area, representing each triangle by a single vertice. This is simple to do, but may generate problems in geometry corners, because no vertices are created there.

Vertice based uses the triangles points positions and then compose the normal and area. This requires informations of adjacent triangles to calculate area and normal. For area, each triangle add it’s area for every vertice in it. For normal, it’s calculated by adding the normal weighted by area of every triangle in which the vertice is used, and then normalizing it.

Representation of vertices in each approach. Blue is central based, red is vertice based.

Nassu uses the central based approach. The vertice approach presented some instabilities in pressure and velocity field when using wall models in IBM.

Triangles area

One important aspect of IBM is the distance between points. The mesh must not be too refined, but also not too coarse. A general recomendation is that the points are evenly spaced and have a distance of 1 between each other.

For central based, we consider the area of a square to facilitate. When considering this, the ideal area is 1 (think of a cartesian grid with distance 1), which presents good results.

For vertice based, we consider an equilateral triangle to calculate the desired area. The area of it is \(\frac{\sqrt{3}}{4}l^2\), substituting \(l=1\) gives \(\frac{\sqrt{3}}{4} \approx 0.433\). So the ideal area is 0.433 for vertice based.

Note

The difference in area of central and vertice based is due to the difference in number of nodes generated. For our use cases, the relation of number of triangles (\(N_t\)) and number of vertices (\(N_v\)) is \(N_t \approx 2N_v\).

So, given the same triangle area, a center based approach produces 2 times the number of vertices than the vertices based approach. This generates vertices that have a smaller area and are closer to each other when comparing center with vertice based approach.

Since the refinement is not perfect, it’s defined an range of area for the triangles, with a minimun and a maximun area. For center based approach, an area range of (0.5, 2) presented good results; for vertice based a range of (0.15, 0.6) presented good results.

Note

Note that the maximun area must be at least 4 times the minimun area.

When refining a triangle with area greater than the maximun, the area is divided in 4. So if the ration is less than that, it’s possible that it generates triangles smaller than the minimun area.