Couette (Startup)

The simulation of a Couette flow is mainly used for validation of the transient flow description through the current collision operator implemented. In this case, the moving wall boundary condition is employed at the \(y=h\) and the halfway bounce-back BC \(y=0\), those BC are therefore also validated.

from nassu.cfg.model import ConfigScheme

filename = "tests/validation/cases/01_couette_flow.nassu.yaml"

sim_cfgs = ConfigScheme.sim_cfgs_from_file_dct(filename)

The simulation parameters are shown below

import pandas as pd
from IPython.display import HTML

sim_cfg = sim_cfgs["startupCouette", 0]
dct = {
    "NX": [sim_cfg.domain.domain_size.x],
    "NY": [sim_cfg.domain.domain_size.y],
    "tau": [sim_cfg.models.LBM.tau],
    "time_steps": sim_cfg.n_steps,
}
df = pd.DataFrame(dct, index=None)

HTML(df.to_html())

	NX	NY	tau	time_steps
0	32	32	0.9	4000

Results

The plots of the evolution of velocity profile compared with the analytical solution are shown below

import matplotlib.pyplot as plt
import numpy as np
from typing import Callable
from nassu.cfg.schemes.simul import SimulationConfigs

Processing functions for Couette Flow case

def get_couette_analytical_func(u_wall: float) -> Callable[[float], float]:
    """Couette analytical velocity function"""
    return lambda pos: u_wall * pos


def get_adimensional_time(sim_cfg: SimulationConfigs, time_step: int) -> float:
    """Adimensional time"""
    nu = sim_cfg.models.LBM.kinematic_viscosity
    h = sim_cfg.domain.domain_size.y
    return nu * time_step / (h**2)


def get_couette_transient_analytical_func(
    sim_cfg: SimulationConfigs, time_step: int, u_wall: float
) -> Callable[[float], float]:
    adim_time = get_adimensional_time(sim_cfg, time_step)

    def func(y: float):
        nonlocal u_wall, adim_time

        fix_term = u_wall * y
        mul_term = 2 * u_wall / np.pi
        terms = []
        for n in range(1, 15):
            exp_term = -(n**2) * (np.pi**2) * adim_time
            sin_term = n * np.pi * (1 - y)
            term = ((-(1**n)) / n) * np.exp(exp_term) * np.sin(sin_term)
            terms.append(term)
        series_sum = sum(terms)
        res = fix_term + mul_term * series_sum
        return res

    return func


def post_proc_couette_time_step(sim_cfg: SimulationConfigs, time_step: int, ax):
    line = sim_cfg.output.series["default"].lines["velocity_profile"]

    points_df = pd.read_csv(line.points_filename)
    data_df = line.read_full_data("ux")

    u_wall = sim_cfg.models.BC.BC_map[0].ux
    adim_time = get_adimensional_time(sim_cfg, time_step)
    transient_func = get_couette_transient_analytical_func(sim_cfg, time_step, u_wall)
    ax.set_title(r"Couette $\nu u/h^2=$" + f"{adim_time:.4f}")

    x_abs = points_df["y"].to_numpy(dtype=np.float32)
    x = (x_abs) / (len(x_abs) - 1)
    num_y = data_df[data_df["time_step"] == time_step]
    num_y = num_y.drop(columns="time_step").to_numpy().T
    ax.plot(x, num_y, "ok", label="Numerical", fillstyle="none")

    analytical_y = transient_func(x)
    ax.plot(x, analytical_y, "--k", label="Analytical")

Process velocity profiles for some time steps

fig, ax = plt.subplots(2, 2)
fig.set_size_inches(12, 9)

time_steps_proc = [80, 400, 800, 4000]
ax_ticks = [0, 0.0005, 0.001, 0.0015, 0.002]
ax_ticks_label = [f"{x:4.1e}" for x in ax_ticks]
for idx, t in enumerate(time_steps_proc):
    i, j = idx % 2, idx // 2
    post_proc_couette_time_step(sim_cfg, t, ax[i, j])
    ax[i, j].set_yticks(ax_ticks)
    ax[i, j].set_yticklabels(ax_ticks_label)
    ax[i, j].legend()


plt.show(fig)

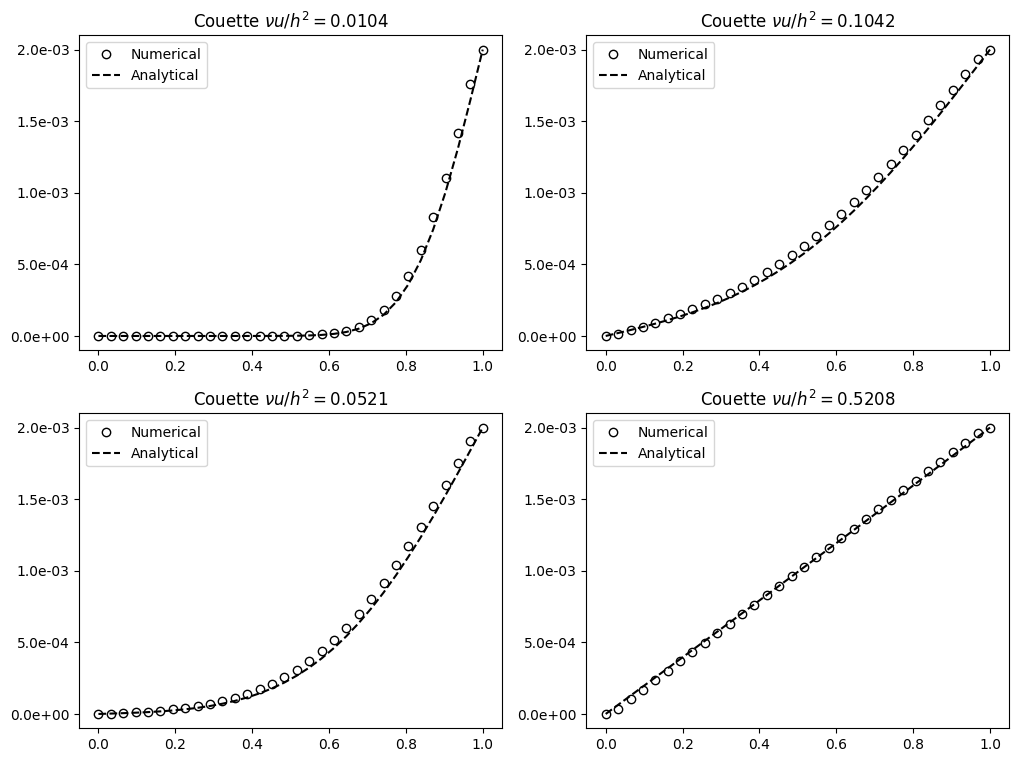
The walls have a slight inaccuracy due to the halfway bounce-back not being “rightly” implemented in moments representation.

Despite that, results show a very satisfatory agreement between numerical model and analytical solution, confirming the solver capability to represent a transient flow.

Version

sim_info = sim_cfg.output.read_info()

nassu_commit = sim_info["commit"]
nassu_version = sim_info["version"]
print("Version:", nassu_version)
print("Commit hash:", nassu_commit)

Version: 

1.6.17
Commit hash: 03afae00d1166dcb73bd88413bb3cfda7b6c686c

Configuration

from IPython.display import Code

Code(filename=filename)

simulations:
  - name: startupCouette
    save_path: ./tests/validation/results/01_couette_flow/startup_couette

    n_steps: 4000

    report:
      frequency: 500

    domain:
      domain_size:
        x: 32
        y: 32
      block_size: 8

    data:
      divergence: { frequency: 50 }
      instantaneous:
        default: { interval: { frequency: 80 }, macrs: [rho, u] }
      statistics:
        interval: { frequency: 0 }
      probes:
        historic_series:
          default:
            interval: { frequency: 80, lvl: 0 }
            macrs: [rho, u]
            lines:
              velocity_profile:
                dist: 1
                start_pos: [4, 0]
                end_pos: [4, 32]

    models:
      precision:
        default: single

      LBM:
        tau: 0.9
        vel_set: D2Q9
        coll_oper: RRBGK

      engine:
        name: CUDA

      BC:
        periodic_dims: [true, false]
        BC_map:
          - pos: N
            BC: VelocityBounceBack
            wall_normal: N
            ux: 2e-3
            uy: 0

          - pos: S
            BC: VelocityBounceBack
            wall_normal: S
            ux: 0
            uy: 0