Introduction#
This user guide is directed towards the use of Nassu LBM solver, which is the backbone of AeroSim digital wind tunnel software. It is CFD solver based on the lattice-Boltzmann method (LBM) to perform wind flow simulations with high performance computing (HPC) by parallel programming for GPU and memory optimization.
Important
This user guide is focused on the Nassu solver and its internals, for our web interface check out our AeroSim documentation.
What is CFD?#
The acronym CFD stands for Computational Fluid Dynamics, the area of knowledge that studies and develops methodologies to numerically solve transport equations such as Navier-Stokes Equations (NSE).
The application of CFD extends from biological systems in hemodynamics, aerodynamics of most varied objects, plastic extrusion in industry, to visual effects in games and movies.

CFD examples in hemodynamics and aerodynamics#
Many methods that numerically solve the NSE are available, when dealing with turbulent flows the most usual are RANS, LES and DNS:

CFD methodologies to solve turbulent flows#
The Reynolds-Averaged-Navier-Stokes (RANS) solves the time-averaged NSE and returns the average properties of the flow. RANS is the most popular CFD method for turbulence due to its low computational cost. However, since in RANS the transient features of the flow are not captured, the method should be applied only to problems in which peak values are not important, which is not the case for wind pressure analysis.
At the other extreme, a Direct Numerical Simulation (DNS) explicitly solves NSE for a given \(\Delta t\) and \(\Delta x\). Great accuracy can be obtained with DNS, however its computational cost is overwhelming for turbulent flow simulations at high Reynolds numbers. Since the method has to capture all turbulent scales to properly reproduce the flow, it requires very fine temporal and spatial resolutions which leads to prohibitive computational costs.
As alternative, Large Eddy Simulations (LES) can be used to satisfactory capture transient aspects of a flow with a viable computational cost. In this methodology, the flow large scales are explicitly solved while the smaller are modelled:
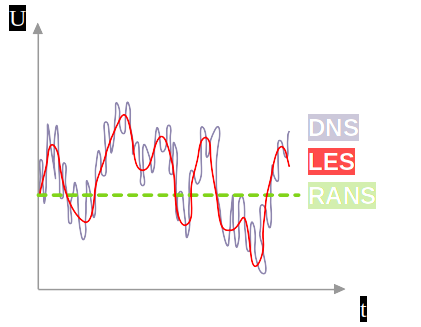
Representation of LES filtering for a velocity signal#
As a result, the macroscopic signals in LES simulations will be smoothed and approach from DNS as spatial and temporal resolutions are increased.
Note
Despite its cost being inferior to DNS, the use of LES for engineering problems is also very computationally demanding, and has only become achievable recently due to constant evolution of computational processing technologies.
CFD as wind engineering tool#
In wind engineering many problems can be approached using CFD when adequates methodology and setup are adopted. In wind tunnel experiments, the pressure fluctuations on the surface of a solid body are measured with a high frequency in order to capture the extreme events that the structure eventually will be subjected to.
To achieve similar results through CFD it is necessary to adopt a method that is transient, and therefore can capture the pressure fluctuations. Wind tunnel experiments for structural design usually occur at a Reynolds numbers above \(10^{5}\), which means that the grid resolution required to represent the small turbulence scales with a DNS would be extremely high and impraticable for most computational resources available.
Hence the usual to approach for such problems would be LES, which can satisfactorily capture the flow statistical behavior (average, variance, kurtosis, and skewness), when a proper setup with adequate boundary conditions, grid refinement and placement of obstacles is estabilished:
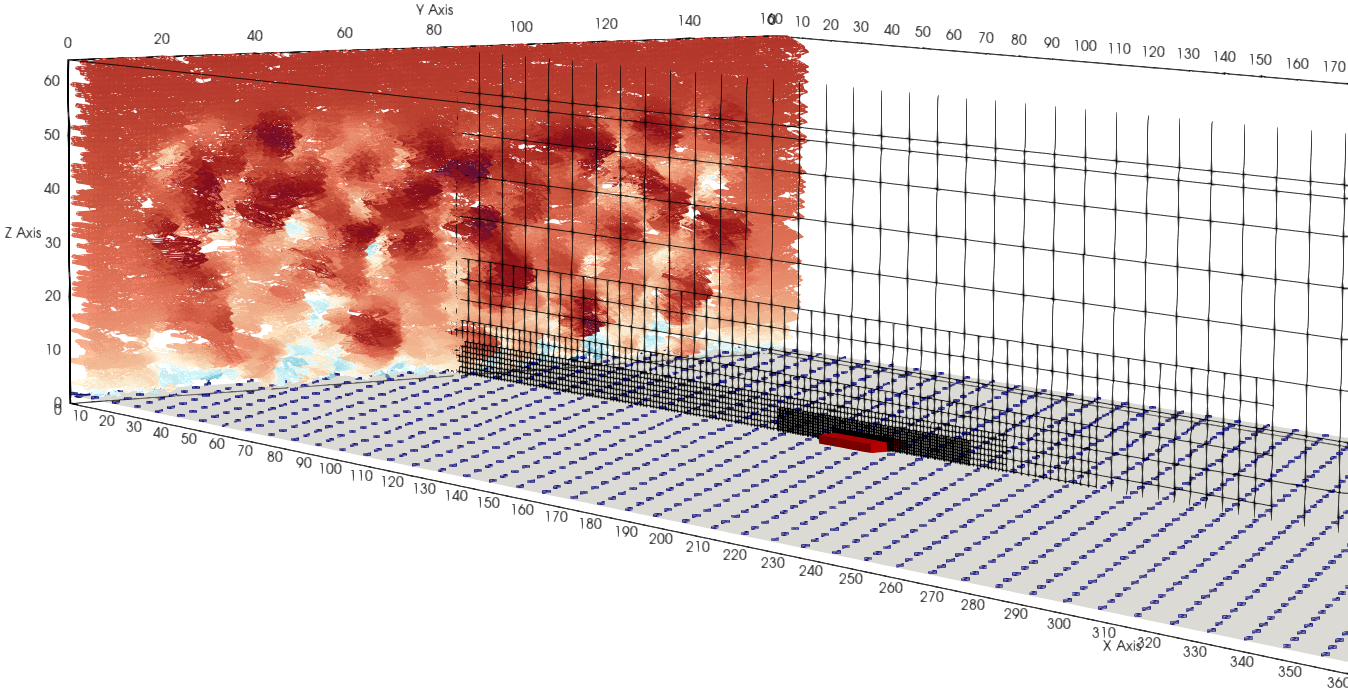
Example of LES wind tunnel setup for a low rise building#
LBM to solve NSE#
As previously stated, the computational cost for LES is still very high. In most LES environments a wind tunnel simulation with adequate resolution and sufficient time interval simulated for statistical analysis would require several days of computing time. This is mostly due to the fact that most LES solvers are based on finite volume methods (FVM). In order to address the same problem in more efficiently, we adopt an alternative paradigm to solve the NSE, which is the lattice-Boltzmann method (LBM).
The LBM is developed from numerical discretization of Boltzmann equation, a partial differential equation (PDE), resulting in the lattice-Boltzmann equation (LBE). Through incompressible assumption, it can be shown that the LBE returns the NSE and hence by solving the LBE, one is solving the NSE from an alternative approach.
The main advantage of the LBM is that its operations occur mostly locally, with only the direct transcription of data series between neighboor nodes. This caracteristic makes the method highly suitable for high performance parallel processing in GPU environments.
Features and performance#
As the LBM only solves for the flow evolution, some other features are still required to proper represent a wind tunnel simulation. In Nassu, some of the features are:
Complex shaped bodies and terrain are represented in computational domain with immersed boundary method (IBM)
A turbulent inlet boundary is implemented with synthetic eddy method (SEM)
Multigrid resolution is adopted near solid bodies
Among other features to enable the capabilities to solve complex aerodynamics problems.
The coupling between LBM and any feature to be implemented will affect the simulation performance overall. Therefore it was also important to optimize the operations related to the features to be implemented in the solver.
Nassu is able to to execute wind tunnel simulations with more than 100M nodes overnight.
Important
A well known bottleneck found in most LBM developments is its memory demand. For that matter, we adopt a macroscopics collision based formulation of the LBM, that eliminates the necessity of saving several population variables for each domain node.
